1368. Minimum Cost to Make at Least One Valid Path in a Grid
Hard
Given a m x n 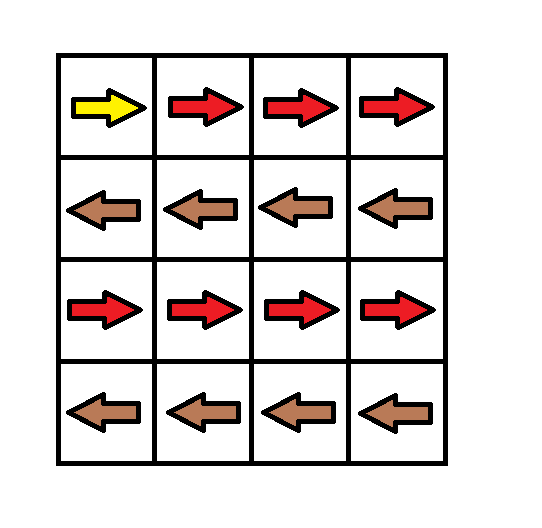
grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:- 1 which means go to the cell to the right. (i.e go from
grid[i][j]togrid[i][j + 1]) - 2 which means go to the cell to the left. (i.e go from
grid[i][j]togrid[i][j - 1]) - 3 which means go to the lower cell. (i.e go from
grid[i][j]togrid[i + 1][j]) - 4 which means go to the upper cell. (i.e go from
grid[i][j]togrid[i - 1][j])
Notice that there could be some invalid signs on the cells of the grid which points outside the grid.
You will initially start at the upper left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path doesn't have to be the shortest.
You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.
Return the minimum cost to make the grid have at least one valid path.
Example 1:

Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]] Output: 3 Explanation: You will start at point (0, 0). The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3) The total cost = 3.
Example 2:

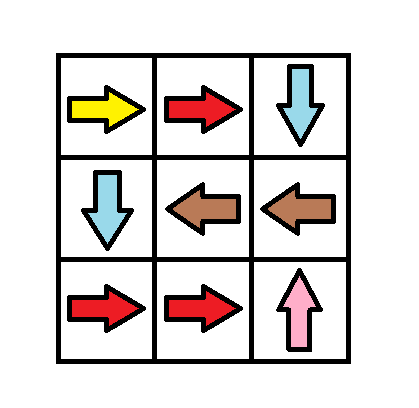
Input: grid = [[1,1,3],[3,2,2],[1,1,4]] Output: 0 Explanation: You can follow the path from (0, 0) to (2, 2).
Example 3:

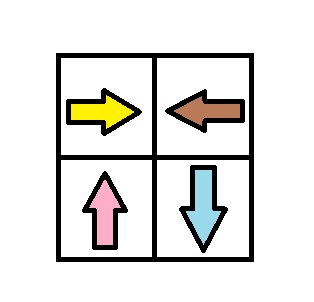
Input: grid = [[1,2],[4,3]] Output: 1
Example 4:
Input: grid = [[2,2,2],[2,2,2]] Output: 3
Example 5:
Input: grid = [[4]] Output: 0
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | class Solution { int m, n; Queue<int[]> bfs = new LinkedList<>(); int[][] DIR = new int[][]{{0,1},{0,-1},{1,0},{-1,0}}; int[][] dp; public int minCost(int[][] grid) { m = grid.length; n = grid[0].length; dp = new int[m][n]; for(int i=0; i<m; ++i){ Arrays.fill(dp[i], -1); } int cost = 0; dfs(grid, 0, 0, cost); while(!bfs.isEmpty()){ int sz = bfs.size(); cost++; for(int i=0; i<sz; ++i){ int[] t = bfs.poll(); for(int[] d:DIR){ dfs(grid, t[0]+d[0], t[1]+d[1], cost); } } } return dp[m-1][n-1]; } void dfs(int[][] grid, int r, int c, int cost){ if(r<0 || r>=m || c<0 || c>=n || dp[r][c]!=-1) return; bfs.add(new int[]{r, c}); dp[r][c] = cost; int next = grid[r][c]-1; dfs(grid, r+DIR[next][0], c+DIR[next][1], cost); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | class Solution { public int minCost(int[][] grid) { int[][] dirs = new int[][] { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } }; int m = grid.length; if (m == 0) return -1; int n = grid[0].length; if (n == 0) return -1; Queue<int[]> que = new LinkedList<>(); que.add(new int[] { 0, 0 }); int[][] cost = new int[m][n];// min cost to get here for (int i = 0; i < m; ++i) Arrays.fill(cost[i], Integer.MAX_VALUE); cost[0][0] = 0; while (!que.isEmpty()) { int[] cell = que.poll(); int r = cell[0], c = cell[1], ct = cost[r][c]; int dir = grid[r][c]; for (int[] d : dirs) { int r1 = r + d[0], c1 = c + d[1]; if (r1 < 0 || r1 >= m || c1 < 0 || c1 >= n) continue; int ct1 = ct + (match(dir, r, c, r1, c1) ? 0 : 1); if (ct1 >= cost[r1][c1]) continue; cost[r1][c1] = ct1; que.add(new int[] { r1, c1 }); } } return cost[m - 1][n - 1]; } boolean match(int d, int r, int c, int r1, int c1) { if (d == 1 && r == r1 && c + 1 == c1) return true; if (d == 2 && r == r1 && c - 1 == c1) return true; if (d == 3 && r + 1 == r1 && c == c1) return true; if (d == 4 && r - 1 == r1 && c == c1) return true; return false; } } |
No comments:
Post a Comment