1377. Frog Position After T Seconds
Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from the vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them with the same probability, otherwise, when the frog can not jump to any unvisited vertex it jumps forever on the same vertex.
The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting directly the vertices fromi and toi.
Return the probability that after t seconds the frog is on the vertex target.
Example 1:
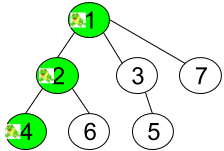
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4 Output: 0.16666666666666666 Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666.
Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7 Output: 0.3333333333333333 Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1.
Example 3:
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6 Output: 0.16666666666666666
Constraints:
1 <= n <= 100edges.length == n-1edges[i].length == 21 <= edges[i][0], edges[i][1] <= n1 <= t <= 501 <= target <= n- Answers within
10^-5of the actual value will be accepted as correct.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | class Solution { public double frogPosition(int n, int[][] edges, int t, int target) { Map<Integer, Set<Integer>> map = new HashMap<>(); for (int[] e : edges) { int u = e[0], v = e[1]; map.computeIfAbsent(u, k -> new HashSet<>()).add(v); map.computeIfAbsent(v, k -> new HashSet<>()).add(u); } Queue<double[]> que = new LinkedList<>(); que.add(new double[] { 1, 1.0 });//node, prob Set<Integer> visited = new HashSet<>(); visited.add(1); int step = 0; boolean found = false; while (!que.isEmpty()) { if (step > t && !found) return 0.0;// haven't found target at t-th second int sz = que.size(); for (int k = 0; k < sz; ++k) { double[] top = que.poll(); int number = (int) top[0]; double p = top[1]; if (number == target) found = true; if (map.containsKey(number)) { Set<Integer> neighbors = map.get(number); Set<Integer> nexts = new HashSet<>(); for (int x : neighbors) { if (!visited.contains(x)) nexts.add(x); } if (step == t && found) return p;//found target at t-th second if (step < t && found && nexts.isEmpty()) return p;//found target before t-th second but it does not have children if (step < t && found && !nexts.isEmpty()) return 0.0;//found target before t-th second and it have children if (!nexts.isEmpty()) { double pNext = p / nexts.size(); for (int nextNumber : nexts) { if (!visited.contains(nextNumber)) { visited.add(nextNumber); que.add(new double[] { nextNumber, pNext }); } } } }else if(found && step<=t) return p;//found target at/before t-th step and there's no further jumps } step++; } return 0.0; } } |
No comments:
Post a Comment