1444. Number of Ways of Cutting a Pizza
Given a rectangular pizza represented as a rows x cols matrix containing the following characters: 'A' (an apple) and '.' (empty cell) and given the integer k. You have to cut the pizza into k pieces using k-1 cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
Return the number of ways of cutting the pizza such that each piece contains at least one apple. Since the answer can be a huge number, return this modulo 10^9 + 7.
Example 1:
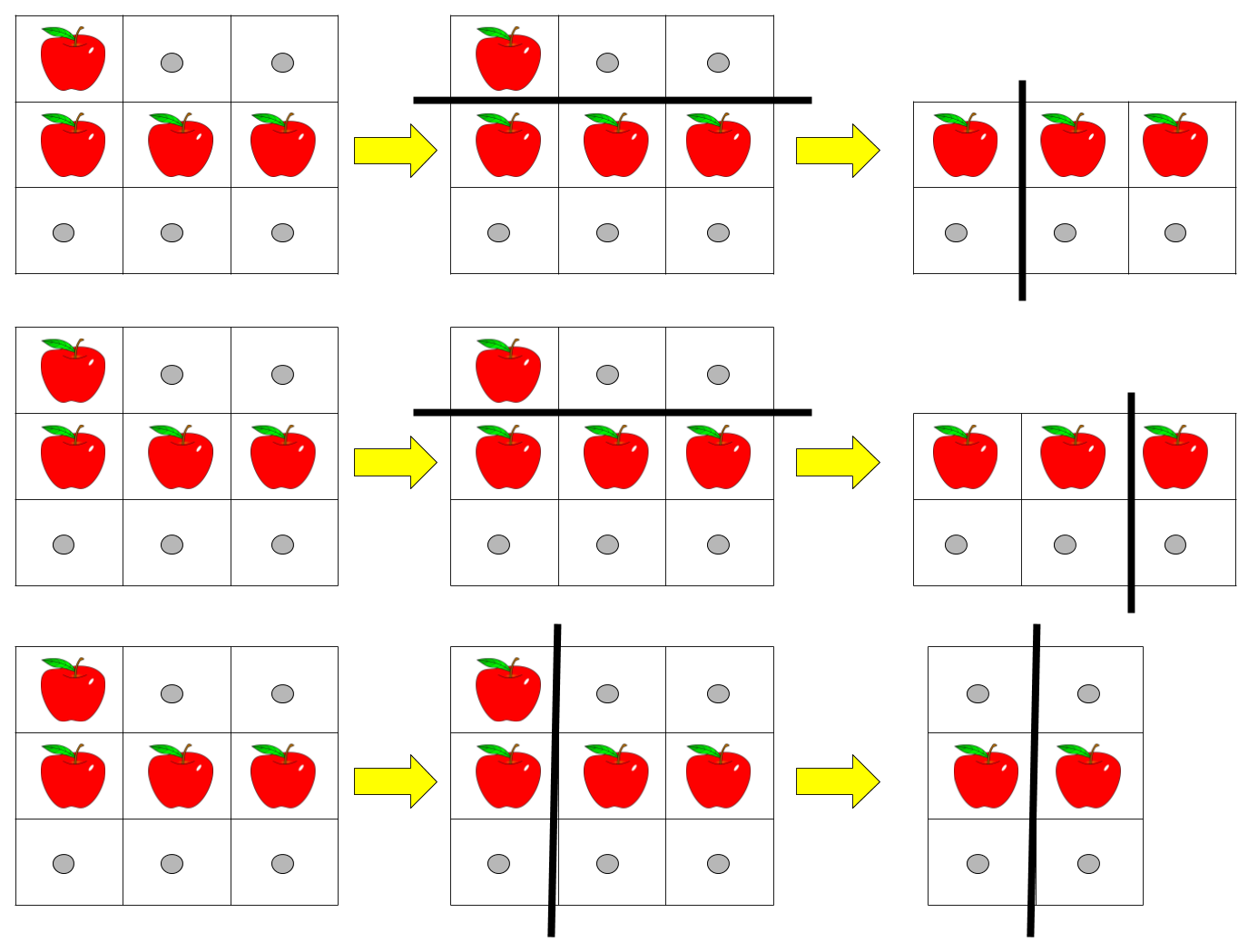
Input: pizza = ["A..","AAA","..."], k = 3 Output: 3 Explanation: The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
Example 2:
Input: pizza = ["A..","AA.","..."], k = 3 Output: 1
Example 3:
Input: pizza = ["A..","A..","..."], k = 1 Output: 1
Constraints:
1 <= rows, cols <= 50rows == pizza.lengthcols == pizza[i].length1 <= k <= 10pizzaconsists of characters'A'and'.'only.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | class Solution { int m, n; Integer[][][] dp;//k, r, c: ways to cut pizze[r:][c:] in k pieces int[][] preSum; int M = 1_000_000_007; public int ways(String[] pizza, int k) { m = pizza.length; n = pizza[0].length(); preSum = new int[m+1][n+1]; for(int i=m-1; i>=0; --i){ for(int j=n-1; j>=0; --j){ preSum[i][j] = preSum[i+1][j]+preSum[i][j+1]-preSum[i+1][j+1]+(pizza[i].charAt(j)=='A'?1:0); } } dp = new Integer[m][n][k]; return dfs(0, 0, k-1); } int dfs(int r, int c, int k){ if(preSum[r][c]==0) return 0; //no apples left => invalide if(k==0) return 1;//found valid way after k-1 cuts; if(dp[r][c][k]!=null) return dp[r][c][k]; int ans = 0; //cut horizontally for(int i = r+1; i<m; ++i){ if(preSum[r][c]-preSum[i][c]>0) ans = (ans + dfs(i, c, k-1))%M; } //cut vertically for(int j = c+1; j<n; ++j){ if(preSum[r][c]-preSum[r][j]>0) ans = (ans + dfs(r, j, k-1))%M; } dp[r][c][k] = ans; return ans; } } |
No comments:
Post a Comment