1326. Minimum Number of Taps to Open to Water a Garden
Hard
There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).
There are n + 1 taps located at points [0, 1, ..., n] in the garden.
Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.
Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.
Example 1:
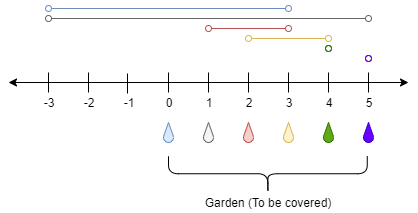
Input: n = 5, ranges = [3,4,1,1,0,0] Output: 1 Explanation: The tap at point 0 can cover the interval [-3,3] The tap at point 1 can cover the interval [-3,5] The tap at point 2 can cover the interval [1,3] The tap at point 3 can cover the interval [2,4] The tap at point 4 can cover the interval [4,4] The tap at point 5 can cover the interval [5,5] Opening Only the second tap will water the whole garden [0,5]
Example 2:
Input: n = 3, ranges = [0,0,0,0] Output: -1 Explanation: Even if you activate all the four taps you cannot water the whole garden.
Example 3:
Input: n = 7, ranges = [1,2,1,0,2,1,0,1] Output: 3
Example 4:
Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4] Output: 2
Example 5:
Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4] Output: 1
Constraints:
1 <= n <= 10^4ranges.length == n + 10 <= ranges[i] <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | class Solution { public int minTaps(int n, int[] ranges) { int[] dp = new int[n+1]; Arrays.fill(dp, Integer.MAX_VALUE); dp[0] = 0; for(int i=0; i<=n; ++i){ int ran = ranges[i]; int l = Math.max(0, i-ran), r = Math.min(n, i+ran); for(int j=l; j<=r; ++j){ if(dp[l]!=Integer.MAX_VALUE) dp[j] = Math.min(dp[j], dp[l]+1); } } return dp[n]==Integer.MAX_VALUE?-1:dp[n]; } } |
No comments:
Post a Comment