LeetCode [850] Rectangle Area II

 850. Rectangle Area II

Hard

We are given a list of (axis-aligned) rectangles.  Each rectangle[i] = [x1, y1, x2, y2] , where (x1, y1) are the coordinates of the bottom-left corner, and (x2, y2) are the coordinates of the top-right corner of the ith rectangle.

Find the total area covered by all rectangles in the plane.  Since the answer may be too large, return it modulo 10^9 + 7.

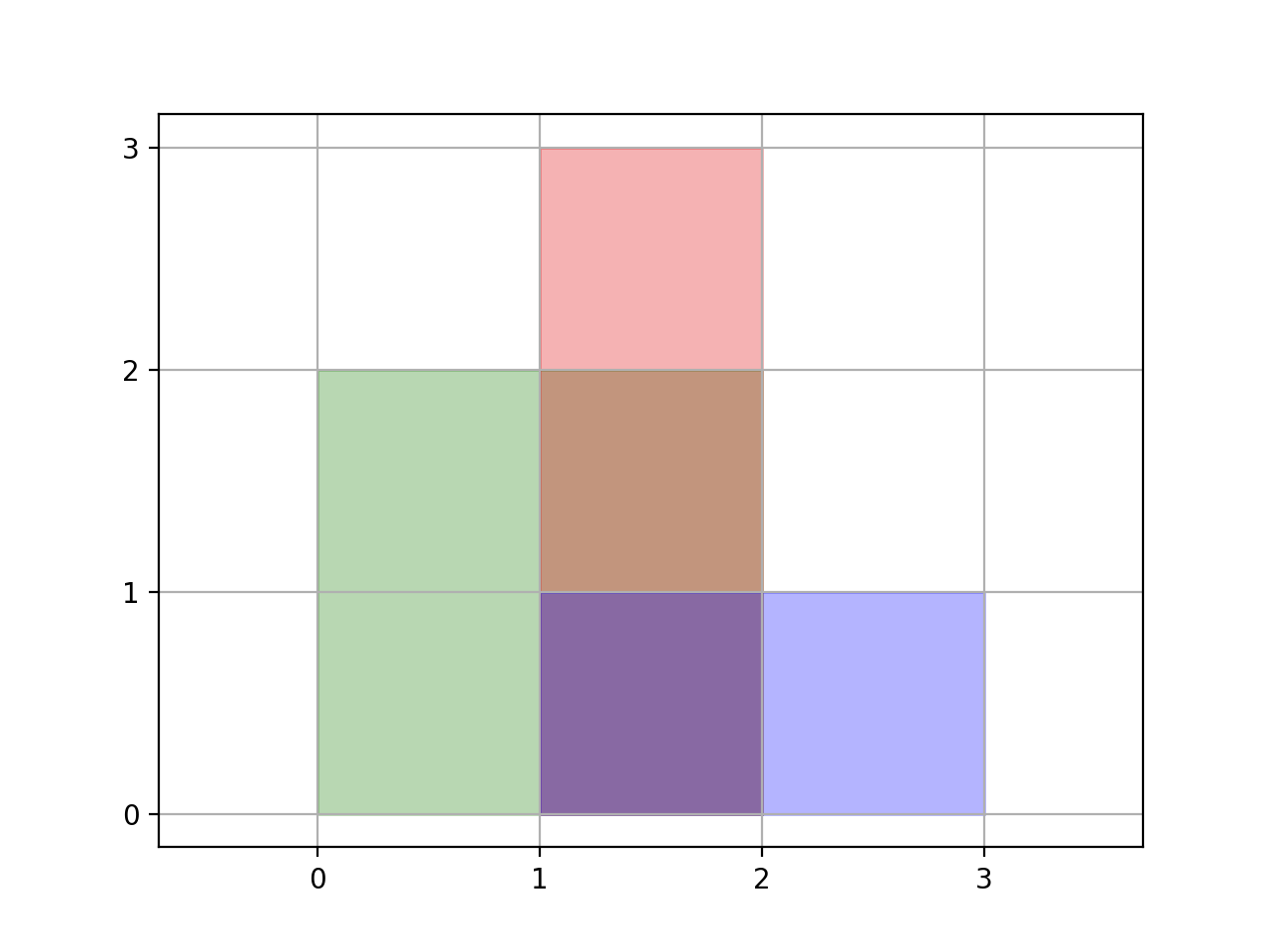
Example 1:

Input: [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
Output: 6
Explanation: As illustrated in the picture.

Example 2:

Input: [[0,0,1000000000,1000000000]]
Output: 49
Explanation: The answer is 10^18 modulo (10^9 + 7), which is (10^9)^2 = (-7)^2 = 49.

Note:

• 1 <= rectangles.length <= 200
• rectanges[i].length = 4
• 0 <= rectangles[i][j] <= 10^9
• The total area covered by all rectangles will never exceed 2^63 - 1 and thus will fit in a 64-bit signed integer.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54

class Solution { public int rectangleArea(int[][] rectangles) { int OPEN = 0, CLOSE = 1; int[][] events = new int[2*rectangles.length][4]; int t = 0; for(int[] rect : rectangles) { events[t++] = new int[]{rect[1], OPEN, rect[0], rect[2]}; events[t++] = new int[]{rect[3], CLOSE, rect[0], rect[2]}; } List<int[]> active = new ArrayList(); Arrays.sort(events, (e1, e2) -> { return Integer.compare(e1[0], e2[0]); }); long ans = 0; int currY = events[0][0]; for(int[] event : events) { int y = event[0]; int state = event[1]; int x1 = event[2]; int x2 = event[3]; long query = 0; int curr = -1; for(int[] activeEvent : active) { curr = Math.max(curr, activeEvent[0]); query += Math.max(activeEvent[1] - curr, 0); curr = Math.max(curr, activeEvent[1]); } ans += query*(y - currY); if(state == OPEN) { active.add(new int[]{x1, x2}); Collections.sort(active, (i1, i2) -> { return Integer.compare(i1[0], i2[0]); }); } else { for(int i=0; i<active.size(); i++) { if (active.get(i)[0] == x1 && active.get(i)[1] == x2) { active.remove(i); break; } } } currY = y; } ans %= 1_000_000_007; return (int)ans; } }