LIKE CODING: LeetCode [109] Convert Sorted List to Binary Search Tree

Friday, February 20, 2015

LeetCode [109] Convert Sorted List to Binary Search Tree

109. Convert Sorted List to Binary Search Tree

Medium

Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example 1:

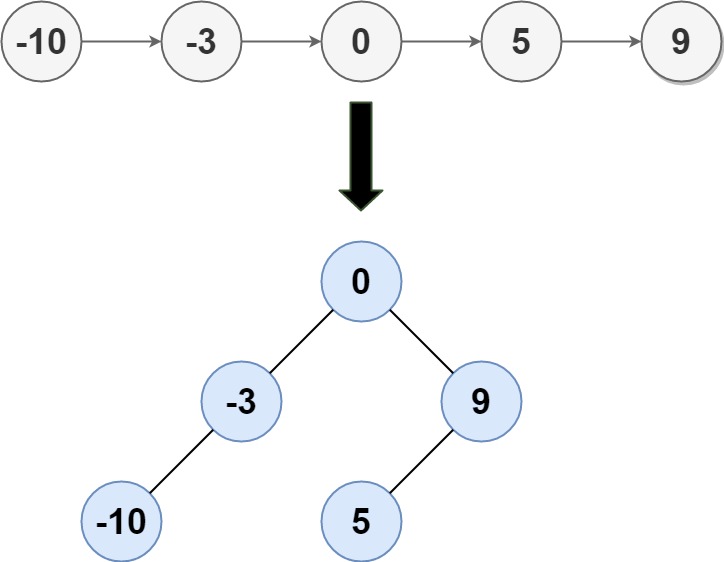
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Example 2:

Input: head = []
Output: []

Example 3:

Input: head = [0]
Output: [0]

Example 4:

Input: head = [1,3]
Output: [3,1]

Constraints:

The number of nodes in head is in the range [0, 2 * 104].
-10^5 <= Node.val <= 10^5

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getLength(ListNode* head){
        int n = 0;
        while(head){
            n++;
            head = head->next;
        }
        return n;
    }

    TreeNode* sortedListToBST(ListNode* head) {
        int n = getLength(head);
        return dfs(head, n);
    }

    TreeNode* dfs(ListNode* &head, int n){
        if(!head||n<=0) return NULL;
        if(n==1){
            TreeNode *node = new TreeNode(head->val);
            head = head->next;
            return node;
        }
        TreeNode* left = dfs(head, (n-1)/2);
        TreeNode* node = new TreeNode(head->val);
        head = head->next;
        TreeNode* right = dfs(head, n-1-(n-1)/2);
        node->left = left;
        node->right = right;
        return node;
    }
};

LIKE CODING

Friday, February 20, 2015

LeetCode [109] Convert Sorted List to Binary Search Tree

No comments:

Post a Comment