LeetCode [1591] Strange Printer II

 1591. Strange Printer II

Hard

There is a strange printer with the following two special requirements:

• On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
• Once the printer has used a color for the above operation, the same color cannot be used again.

You are given a m x n matrix targetGrid, where targetGrid[row][col] is the color in the position (row, col) of the grid.

Return true if it is possible to print the matrix targetGrid, otherwise, return false.

 

Example 1:

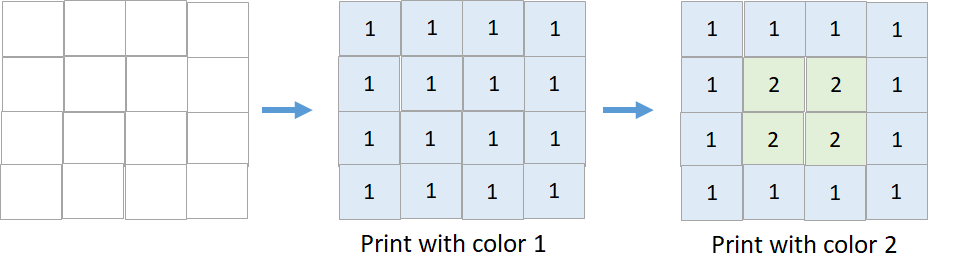
Input: targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
Output: true

Example 2:

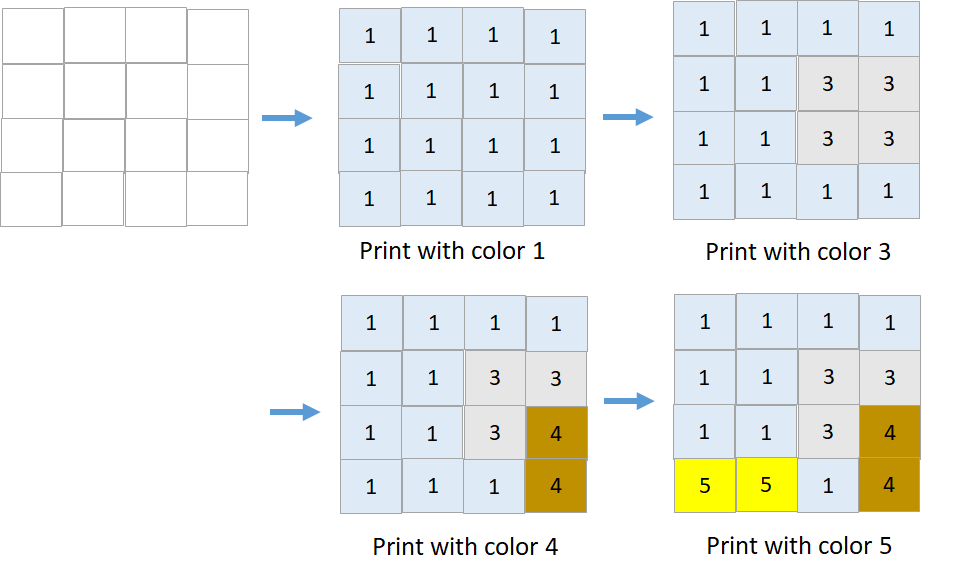
Input: targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
Output: true

Example 3:

Input: targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
Output: false
Explanation: It is impossible to form targetGrid because it is not allowed to print the same color in different turns.

Example 4:

Input: targetGrid = [[1,1,1],[3,1,3]]
Output: false

 

Constraints:

• m == targetGrid.length
• n == targetGrid[i].length
• 1 <= m, n <= 60
• 1 <= targetGrid[row][col] <= 60

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

class Solution { public boolean isPrintable(int[][] targetGrid) { int m = targetGrid.length, n = targetGrid[0].length; int[][] pos = new int[61][4];//[i0, j0, i1, j1] for(int i=0; i<60; ++i) Arrays.fill(pos[i], -1); Set<Integer> colors = new HashSet<>(); for(int i=0; i<m; ++i){ for(int j=0; j<n; ++j){ int c = targetGrid[i][j]; colors.add(c); pos[c][0] = pos[c][0]==-1 ? i : Math.min(pos[c][0], i); pos[c][1] = pos[c][1]==-1 ? j : Math.min(pos[c][1], j); pos[c][2] = pos[c][2]==-1 ? i : Math.max(pos[c][2], i); pos[c][3] = pos[c][3]==-1 ? j : Math.max(pos[c][3], j); } } boolean cont = true; while(cont && !colors.isEmpty()){ cont = false; Set<Integer> tmp = new HashSet<>(colors); for(int c : colors){ if(isOneColor(pos[c][0], pos[c][1], pos[c][2], pos[c][3], targetGrid, c)){ tmp.remove(c); cont = true; } } colors = tmp; } return colors.isEmpty(); } boolean isOneColor(int i0, int j0, int i1, int j1, int[][] targetGrid, int c){ for(int i=i0; i<=i1; ++i){ for(int j=j0; j<=j1; ++j){ if(targetGrid[i][j]>0 && targetGrid[i][j]!=c) return false; } } //if is one color, marked 0 for uncoloring for(int i=i0; i<=i1; ++i){ for(int j=j0; j<=j1; ++j){ targetGrid[i][j] = 0; } } return true; } }