LeetCode [1631] Path With Minimum Effort

 1631. Path With Minimum Effort

Medium

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

 

Example 1:

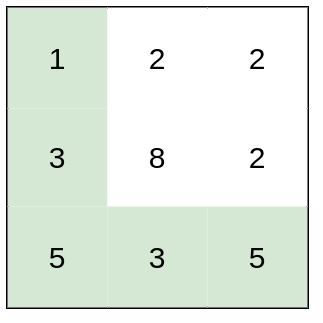
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

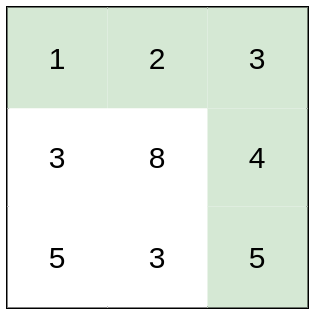
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

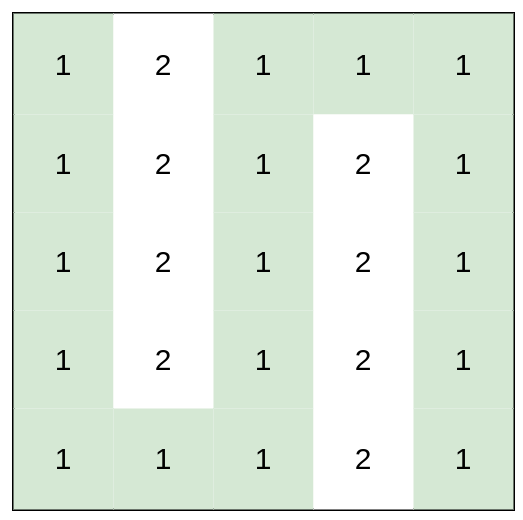
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

 

Constraints:

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

class Solution { int[][] dir = new int[][]{{-1,0},{1,0},{0,-1},{0,1}}; public int minimumEffortPath(int[][] heights) { int m = heights.length; if(m==0) return 0; int n = heights[0].length; if(n==0) return 0; int[][] dist = new int[m][n]; for(int i=0; i<m; ++i){ Arrays.fill(dist[i], Integer.MAX_VALUE); } //dist, r, c PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> a[0]-b[0]); pq.add(new int[]{0,0,0}); while(!pq.isEmpty()){ int[] top = pq.poll(); int d = top[0], r = top[1], c = top[2]; if(d<dist[r][c]){ dist[r][c] = d; for(int[] di : dir){ int nr = r + di[0], nc = c + di[1]; if(nr>=0 && nr<m && nc>=0 && nc<n){ int diff = Math.abs(heights[r][c]-heights[nr][nc]); int newHeight = Math.max(d, diff); if(newHeight<dist[nr][nc]){ pq.add(new int[]{newHeight, nr, nc}); } } } } } return dist[m-1][n-1]; } }