LeetCode [1259] Handshakes That Don't Cross

1259. Handshakes That Don't Cross

Hard

You are given an even number of people num_people that stand around a circle and each person shakes hands with someone else, so that there are num_people / 2 handshakes total.

Return the number of ways these handshakes could occur such that none of the handshakes cross.

Since this number could be very big, return the answer mod 10^9 + 7

 

Example 1:

Input: num_people = 2
Output: 1

Example 2:

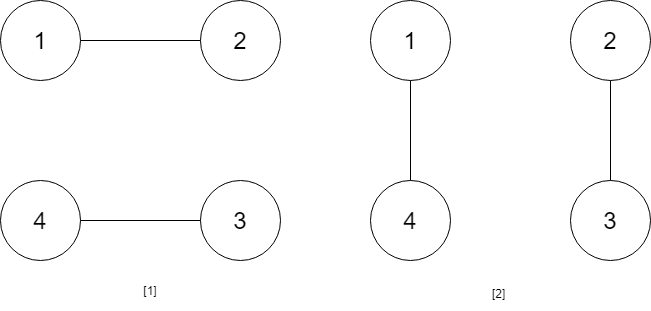
Input: num_people = 4
Output: 2
Explanation: There are two ways to do it, the first way is [(1,2),(3,4)] and the second one is [(2,3),(4,1)].

Example 3:

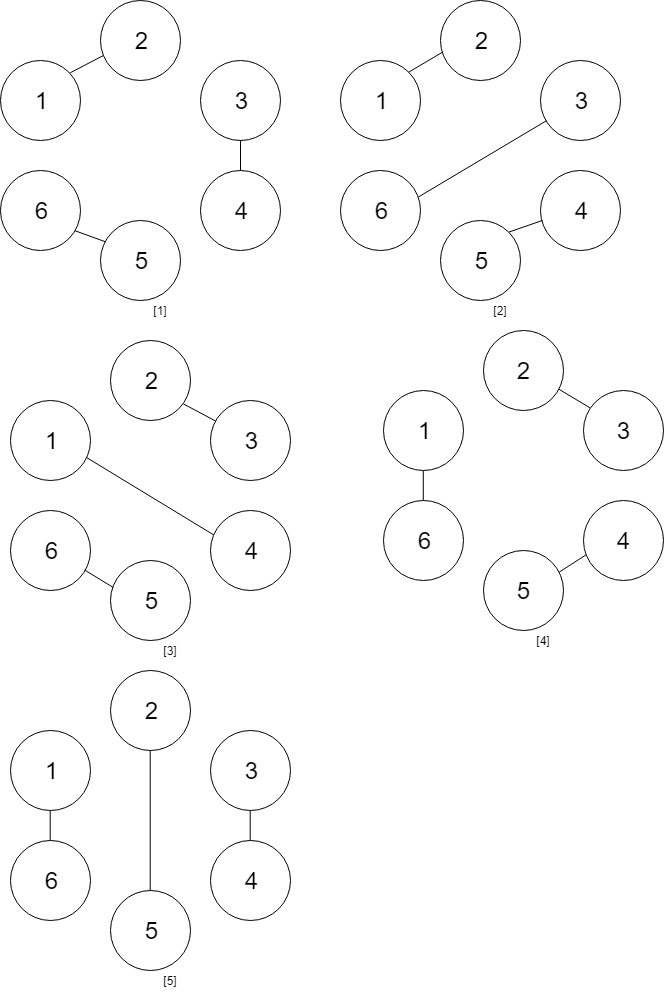
Input: num_people = 6
Output: 5

Example 4:

Input: num_people = 8
Output: 14

 

Constraints:

• 2 <= num_people <= 1000
• num_people % 2 == 0

1 2 3 4 5 6 7 8 9 10 11 12 13

class Solution { public int numberOfWays(int n) { long mod = (long)1e9 + 7; long[] dp = new long[n / 2 + 1]; dp[0] = 1; for (int k = 1; k <= n / 2; ++k) { for (int i = 0; i < k; ++i) { dp[k] = (dp[k] + dp[i] * dp[k - 1 - i]) % mod; } } return (int)dp[n / 2]; } }