LeetCode [986] Interval List Intersections

986. Interval List Intersections

Medium

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.  The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval.  For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

 

Example 1:

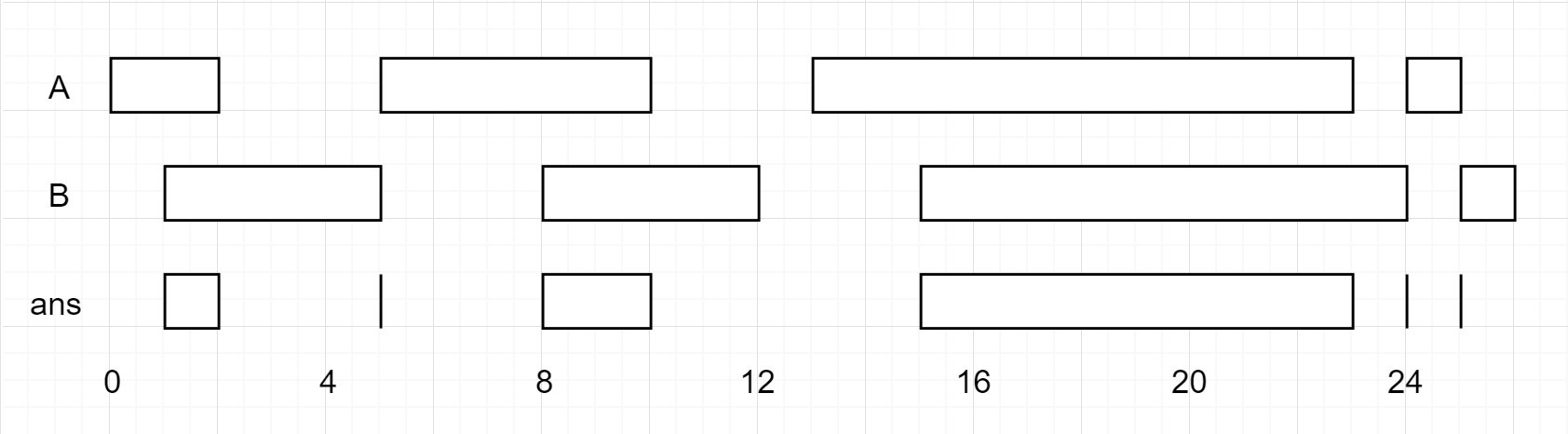
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

 

Note:

1. 0 <= A.length < 1000
2. 0 <= B.length < 1000
3. 0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

class Solution { public: vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) { int i = 0, j = 0, sa = A.size(), sb = B.size(); vector<vector<int>> ret; while(i<sa && j<sb) { if(A[i][1]<B[j][0]){ i++; }else if(B[j][1]<A[i][0]){ j++; }else{ int l = max(A[i][0], B[j][0]); int r = min(A[i][1], B[j][1]); ret.push_back(vector<int>{l, r}); if(A[i][1]>B[j][1]) j++; else i++; } } return ret; } };

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

//Java class Solution { public int[][] intervalIntersection(int[][] A, int[][] B) { if(A==null || A.length==0 || B==null || B.length==0) return new int[0][]; int m = A.length, n = B.length; int i = 0, j = 0; List<int[]> ret = new ArrayList<>(); while(i<m && j<n){ if(A[i][1]<B[j][0]) i++; else if(B[j][1]<A[i][0]) j++; else{ int l = Math.max(A[i][0], B[j][0]); int r = Math.min(A[i][1], B[j][1]); ret.add(new int[]{l, r}); if(A[i][1]<B[j][1]) i++; else j++; } } return ret.toArray(new int[0][]); } }