LIKE CODING: March 2021

Wednesday, March 31, 2021

LeetCode [1610] Maximum Number of Visible Points

1610. Maximum Number of Visible Points

Hard

You are given an array points, an integer angle, and your location, where location = [posx, posy] and points[i] = [xi, yi] both denote integral coordinates on the X-Y plane.

Initially, you are facing directly east from your position. You cannot move from your position, but you can rotate. In other words, posx and posy cannot be changed. Your field of view in degrees is represented by angle, determining how wide you can see from any given view direction. Let d be the amount in degrees that you rotate counterclockwise. Then, your field of view is the inclusive range of angles [d - angle/2, d + angle/2].

You can see some set of points if, for each point, the angle formed by the point, your position, and the immediate east direction from your position is in your field of view.

There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.

Return the maximum number of points you can see.

Example 1:

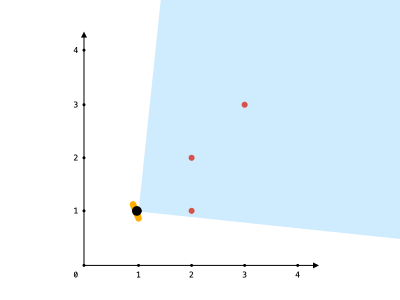
Input: points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
Output: 3
Explanation: The shaded region represents your field of view. All points can be made visible in your field of view, including [3,3] even though [2,2] is in front and in the same line of sight.

Example 2:

Input: points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
Output: 4
Explanation: All points can be made visible in your field of view, including the one at your location.

Example 3:

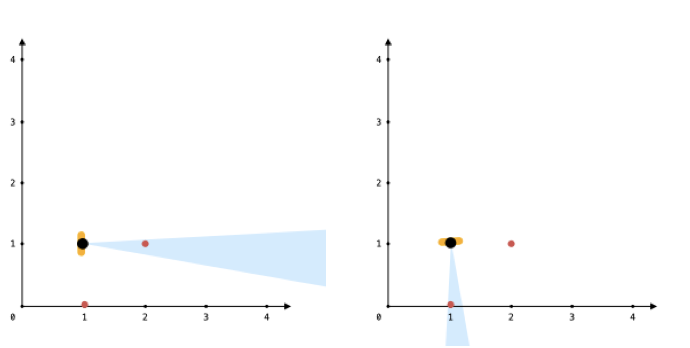
Input: points = [[1,0],[2,1]], angle = 13, location = [1,1]
Output: 1
Explanation: You can only see one of the two points, as shown above.

Constraints:

1 <= points.length <= 105
points[i].length == 2
location.length == 2
0 <= angle < 360
0 <= posx, posy, xi, yi <= 100

Accepted

7,207

Submissions

23,791

class Solution {
    public int visiblePoints(List<List<Integer>> points, int angle, List<Integer> location) {
        int n = points.size();
        List<Double> degress = new ArrayList<>();
        int origins = 0;
        for(List<Integer> point : points){
            int x = point.get(0) - location.get(0);
            int y = point.get(1) - location.get(1);
            double d = 0;
            if(x==0){
                if(y==0) origins++;
                else if(y>0) d = 90;
                else d = 270;
            }else{
                d = Math.toDegrees(Math.atan(y/(double)x));
                if(x<0 && y>=0) d = 180 + d;//2
                else if(x<0 && y<0) d = 180+d;//3
                else if(x>0 && y<0) d = 360+d;//4
            }
            if(x!=0 || y!=0) degress.add(d);
        }

        n = degress.size();
        for(int i=n; i<2*n; ++i) degress.add(degress.get(i-n)+360);
        Collections.sort(degress);
        
        int l = 0, r = 0;
        int max = 0;
        while(r<2*n){
            while(r<2*n && degress.get(r)-degress.get(l)<=angle) r++;
            max = Math.max(r-l, max);
            l++;
        }
        return max+origins;
    }
}

Tuesday, March 23, 2021

LeetCode [920] Number of Music Playlists

920. Number of Music Playlists

Hard

Your music player contains N different songs and she wants to listen to L (not necessarily different) songs during your trip. You create a playlist so that:

Every song is played at least once
A song can only be played again only if K other songs have been played

Return the number of possible playlists. As the answer can be very large, return it modulo 10^9 + 7.

Example 1:

Input: N = 3, L = 3, K = 1
Output: 6
Explanation: There are 6 possible playlists. [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1].

Example 2:

Input: N = 2, L = 3, K = 0
Output: 6
Explanation: There are 6 possible playlists. [1, 1, 2], [1, 2, 1], [2, 1, 1], [2, 2, 1], [2, 1, 2], [1, 2, 2]

Example 3:

Input: N = 2, L = 3, K = 1
Output: 2
Explanation: There are 2 possible playlists. [1, 2, 1], [2, 1, 2]

Note:

0 <= K < N <= L <= 100

Accepted

13,936

Submissions

29,137

class Solution {
    long M = 1000000000+7;
    public int numMusicPlaylists(int N, int L, int K) {
        long[][] dp = new long[L][N];

        for(int j=0; j<N; ++j){
            dp[0][j] = j==0?N:0;
        }

        for(int i=1; i<L; ++i){
            dp[i][0] = K==0?N:0;
        }

        for(int i=1; i<L; ++i){
            for(int j=1; j<N; ++j){
                dp[i][j] = dp[i-1][j-1]*(N-j)%M;
                if(j+1-K>0) dp[i][j] = (dp[i][j] + dp[i-1][j]*(j+1-K)%M)%M;
            }
        }

        return (int)dp[L-1][N-1];
    }
}

LeetCode [488]

488. Zuma Game

Hard

Think about Zuma Game. You have a row of balls on the table, colored red(R), yellow(Y), blue(B), green(G), and white(W). You also have several balls in your hand.

Each time, you may choose a ball in your hand, and insert it into the row (including the leftmost place and rightmost place). Then, if there is a group of 3 or more balls in the same color touching, remove these balls. Keep doing this until no more balls can be removed.

Find the minimal balls you have to insert to remove all the balls on the table. If you cannot remove all the balls, output -1.

Example 1:

Input: board = "WRRBBW", hand = "RB"
Output: -1
Explanation: WRRBBW -> WRR[R]BBW -> WBBW -> WBB[B]W -> WW

Example 2:

Input: board = "WWRRBBWW", hand = "WRBRW"
Output: 2
Explanation: WWRRBBWW -> WWRR[R]BBWW -> WWBBWW -> WWBB[B]WW -> WWWW -> empty

Example 3:

Input: board = "G", hand = "GGGGG"
Output: 2
Explanation: G -> G[G] -> GG[G] -> empty

Example 4:

Input: board = "RBYYBBRRB", hand = "YRBGB"
Output: 3
Explanation: RBYYBBRRB -> RBYY[Y]BBRRB -> RBBBRRB -> RRRB -> B -> B[B] -> BB[B] -> empty

Constraints:

You may assume that the initial row of balls on the table won’t have any 3 or more consecutive balls with the same color.
1 <= board.length <= 16
1 <= hand.length <= 5
Both input strings will be non-empty and only contain characters 'R','Y','B','G','W'.

class Solution {
    int minOp = Integer.MAX_VALUE;
    Set<String> set = new HashSet<>();
    public int findMinStep(String board, String hand) {
        helper(board, hand, 0);
        return minOp == Integer.MAX_VALUE ? -1 : minOp;
    }

    void helper(String b, String h, int op) {
        set.add(new String(b+" "+h));
        if (op >= minOp) return;
        if (b.length() == 0) {
            minOp = Math.min(op, minOp);
            return;
        }

        for (int i = 0; i <= b.length(); ++i) {
            for (int j = 0; j < h.length(); ++j) {
                String b1 = b.substring(0, i) + h.substring(j, j + 1) + b.substring(i);
                String h1 = h.substring(0, j) + h.substring(j + 1);
                boolean cont = true;
                while (cont) {
                    cont = false;
                    int l = 0, r = 0;
                    while (l < b1.length()) {
                        r = l;
                        while (r < b1.length() && b1.charAt(l) == b1.charAt(r)) r++;
                        if (r - l >= 3) {
                            b1 = b1.substring(0, l) + b1.substring(r);
                            cont = true;
                        }
                        l = r;
                    }
                }
                String key = b1+" "+h1;
                if(!set.contains(key)) helper(b1, h1, op + 1);
            }
        }

    }
}

Monday, March 22, 2021

LeetCode [1492] The kth Factor of n

1492. The kth Factor of n

Medium

Given two positive integers n and k.

A factor of an integer n is defined as an integer i where n % i == 0.

Consider a list of all factors of n sorted in ascending order, return the kth factor in this list or return -1 if n has less than k factors.

Example 1:

Input: n = 12, k = 3
Output: 3
Explanation: Factors list is [1, 2, 3, 4, 6, 12], the 3rd factor is 3.

Example 2:

Input: n = 7, k = 2
Output: 7
Explanation: Factors list is [1, 7], the 2nd factor is 7.

Example 3:

Input: n = 4, k = 4
Output: -1
Explanation: Factors list is [1, 2, 4], there is only 3 factors. We should return -1.

Example 4:

Input: n = 1, k = 1
Output: 1
Explanation: Factors list is [1], the 1st factor is 1.

Example 5:

Input: n = 1000, k = 3
Output: 4
Explanation: Factors list is [1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000].

Constraints:

1 <= k <= n <= 1000

class Solution {
    public int kthFactor(int n, int k) {
        if(k==1) return 1;
        
        int cnt = 0;
        for(int d = 1; d<=n/2; ++d){
            if(n%d==0){
                if(++cnt==k) return d;
            } 
        }
        
        if(cnt+1==k) return n;
        return -1;
    }
}

Friday, March 19, 2021

LeetCode [724] Find Pivot Index

724. Find Pivot Index

Easy

Given an array of integers nums, calculate the pivot index of this array.

The pivot index is the index where the sum of all the numbers strictly to the left of the index is equal to the sum of all the numbers strictly to the index's right.

If the index is on the left edge of the array, then the left sum is 0 because there are no elements to the left. This also applies to the right edge of the array.

Return the leftmost pivot index. If no such index exists, return -1.

Example 1:

Input: nums = [1,7,3,6,5,6]
Output: 3
Explanation:
The pivot index is 3.
Left sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11
Right sum = nums[4] + nums[5] = 5 + 6 = 11

Example 2:

Input: nums = [1,2,3]
Output: -1
Explanation:
There is no index that satisfies the conditions in the problem statement.

Example 3:

Input: nums = [2,1,-1]
Output: 0
Explanation:
The pivot index is 0.
Left sum = 0 (no elements to the left of index 0)
Right sum = nums[1] + nums[2] = 1 + -1 = 0

class Solution {
    public int pivotIndex(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        for(int i=0; i<n; ++i){
            dp[i] = nums[i] + (i==0?0:dp[i-1]);
        }
        
        for(int i=0; i<n; ++i){
            int left = i==0?0:dp[i-1];
            int right = dp[n-1]-dp[i];
            if(left==right) return i;
        }
        
        return -1;
    }
}