LeetCode [1697] Checking Existence of Edge Length Limited Paths

 1697. Checking Existence of Edge Length Limited Paths

Hard

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.

Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qj such that each edge on the path has a distance strictly less than limitj .

Return a boolean array answer, where answer.length == queries.length and the jth value of answer is true if there is a path for queries[j] is true, and false otherwise.

 

Example 1:

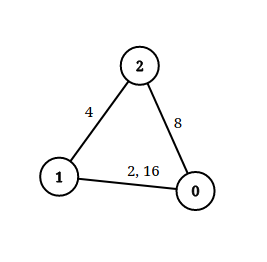
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.

Example 2:

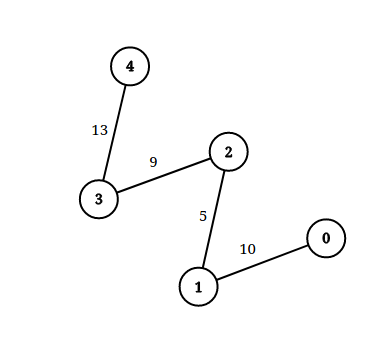
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Exaplanation: The above figure shows the given graph.

 

Constraints:

• 2 <= n <= 105
• 1 <= edgeList.length, queries.length <= 105
• edgeList[i].length == 3
• queries[j].length == 3
• 0 <= ui, vi, pj, qj <= n - 1
• ui != vi
• pj != qj
• 1 <= disi, limitj <= 109
• There may be multiple edges between two nodes.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

class Solution { public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) { int[] p = new int[n]; for(int i=0; i<n; ++i) p[i] = i; Arrays.sort(edgeList, (a, b) -> a[2]-b[2]); int szQ = queries.length; int szE = edgeList.length; boolean[] ret = new boolean[szQ]; int[][] queries1 = new int[szQ][4]; for(int i=0; i<szQ; ++i){ queries1[i][0] = queries[i][0]; queries1[i][1] = queries[i][1]; queries1[i][2] = queries[i][2]; queries1[i][3] = i; } Arrays.sort(queries1, (a, b) -> a[2]-b[2]); int idQ = 0; int idE = 0; while(idQ < szQ){ int limit = queries1[idQ][2]; while(idE < szE && edgeList[idE][2]<limit){ int u = edgeList[idE][0]; int v = edgeList[idE][1]; int x = find(u, p); int y = find(v, p); p[y] = x; idE++; } int p1 = find(queries1[idQ][0], p); int p2 = find(queries1[idQ][1], p); ret[queries1[idQ][3]] = p1==p2; idQ++; } return ret; } int find(int x, int[] p){ while(x!=p[x]) return find(p[x], p); return x; } }