LeetCode [934] Shortest Bridge

934. Shortest Bridge

Medium

In a given 2D binary array A, there are two islands.  (An island is a 4-directionally connected group of 1s not connected to any other 1s.)

Now, we may change 0s to 1s so as to connect the two islands together to form 1 island.

Return the smallest number of 0s that must be flipped.  (It is guaranteed that the answer is at least 1.)

 

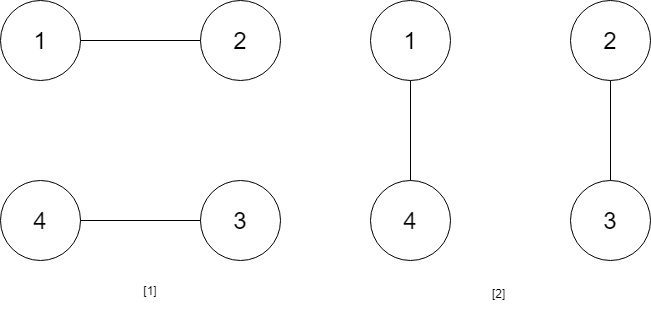
Example 1:

Input: A = [[0,1],[1,0]]
Output: 1

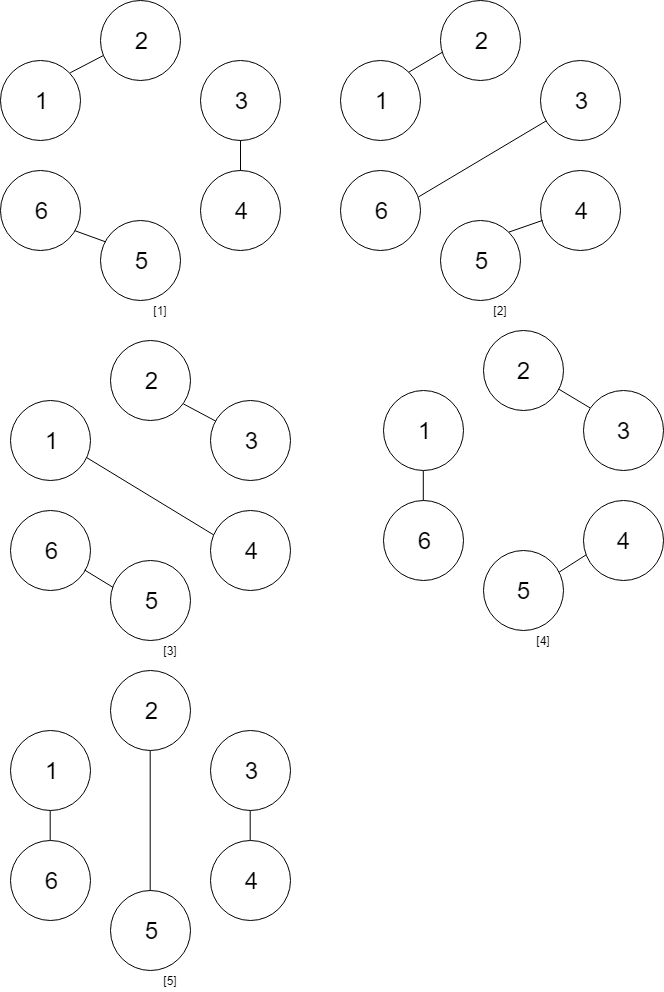
Example 2:

Input: A = [[0,1,0],[0,0,0],[0,0,1]]
Output: 2

Example 3:

Input: A = [[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
Output: 1

 

Constraints:

• 2 <= A.length == A[0].length <= 100
• A[i][j] == 0 or A[i][j] == 1

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

class Solution { public: int paint(vector<vector<int>>& A, int i, int j) { if (i < 0 || j < 0 || i == A.size() || j == A.size() || A[i][j] != 1) return 0; A[i][j] = 2; return 1 + paint(A, i + 1, j) + paint(A, i - 1, j) + paint(A, i, j + 1) + paint(A, i, j - 1); } bool expand(vector<vector<int>>& A, int i, int j, int cl) { if (i < 0 || j < 0 || i == A.size() || j == A.size()) return false; if (A[i][j] == 0) A[i][j] = cl + 1; return A[i][j] == 1; } int shortestBridge(vector<vector<int>>& A) { for (int i = 0, found = 0; !found && i < A.size(); ++i) for (int j = 0; !found && j < A[0].size(); ++j) found = paint(A, i, j); for (int cl = 2; ; ++cl) for (int i = 0; i < A.size(); ++i) for (int j = 0; j < A.size(); ++j) if (A[i][j] == cl && ((expand(A, i - 1, j, cl) || expand(A, i, j - 1, cl) || expand(A, i + 1, j, cl) || expand(A, i, j + 1, cl)))) return cl - 2; } };

LeetCode [1259] Handshakes That Don't Cross

1259. Handshakes That Don't Cross

Hard

You are given an even number of people num_people that stand around a circle and each person shakes hands with someone else, so that there are num_people / 2 handshakes total.

Return the number of ways these handshakes could occur such that none of the handshakes cross.

Since this number could be very big, return the answer mod 10^9 + 7

 

Example 1:

Input: num_people = 2
Output: 1

Example 2:

Input: num_people = 4
Output: 2
Explanation: There are two ways to do it, the first way is [(1,2),(3,4)] and the second one is [(2,3),(4,1)].

Example 3:

Input: num_people = 6
Output: 5

Example 4:

Input: num_people = 8
Output: 14

 

Constraints:

• 2 <= num_people <= 1000
• num_people % 2 == 0

1 2 3 4 5 6 7 8 9 10 11 12 13

class Solution { public int numberOfWays(int n) { long mod = (long)1e9 + 7; long[] dp = new long[n / 2 + 1]; dp[0] = 1; for (int k = 1; k <= n / 2; ++k) { for (int i = 0; i < k; ++i) { dp[k] = (dp[k] + dp[i] * dp[k - 1 - i]) % mod; } } return (int)dp[n / 2]; } }

KMP

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

package KMP; public class Main { public static void main(String[] args) { System.out.println("KMP"); KMP kmp = new KMP("THIS IS A TEST TEXT", "TEST"); kmp.search(); KMP kmp1 = new KMP("AABAACAADAABAABA", "AABA"); kmp1.search(); } } class KMP{ String texts = ""; String pattern = ""; int nt, np; int[] lps; KMP(String t, String p){ texts = t; pattern = p; nt = texts.length(); np = pattern.length(); lps = new int[np]; } void preProcess(){ for(int i=1; i<np; ++i){ int l = lps[i-1]; while(l>0 && pattern.charAt(i)!=pattern.charAt(l)){ l = lps[l-1]; } if(pattern.charAt(l)==pattern.charAt(i)){ lps[i] = l+1; } } } void search(){ preProcess(); int i = 0, j = 0; while(i<nt && j<np){ if(texts.charAt(i)!=pattern.charAt(j)){ i++; j = lps[j]; }else{ if(j==np-1){ System.out.println(i+1-np); i++; j = lps[j]; }else{ i++; j++; } } } } }

LeetCode [403] Frog Jump

 403. Frog Jump

Hard

A frog is crossing a river. The river is divided into x units and at each unit there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.

Given a list of stones' positions (in units) in sorted ascending order, determine if the frog is able to cross the river by landing on the last stone. Initially, the frog is on the first stone and assume the first jump must be 1 unit.

If the frog's last jump was k units, then its next jump must be either k - 1, k, or k + 1 units. Note that the frog can only jump in the forward direction.

Note:

• The number of stones is ≥ 2 and is < 1,100.
• Each stone's position will be a non-negative integer < 231.
• The first stone's position is always 0.

Example 1:

[0,1,3,5,6,8,12,17]

There are a total of 8 stones.
The first stone at the 0th unit, second stone at the 1st unit,
third stone at the 3rd unit, and so on...
The last stone at the 17th unit.

Return true. The frog can jump to the last stone by jumping 
1 unit to the 2nd stone, then 2 units to the 3rd stone, then 
2 units to the 4th stone, then 3 units to the 6th stone, 
4 units to the 7th stone, and 5 units to the 8th stone.

Example 2:

[0,1,2,3,4,8,9,11]

Return false. There is no way to jump to the last stone as 
the gap between the 5th and 6th stone is too large.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

//The key of the map is stone. The value is, if the frog stand on this stone, how many steps this frog can jump. class Solution { public boolean canCross(int[] stones) { if (stones.length == 0) { return true; } HashMap<Integer, HashSet<Integer>> map = new HashMap<Integer, HashSet<Integer>>(stones.length); map.put(0, new HashSet<Integer>()); map.get(0).add(1); for (int i = 1; i < stones.length; i++) { map.put(stones[i], new HashSet<Integer>() ); } for (int i = 0; i < stones.length - 1; i++) { int stone = stones[i]; for (int step : map.get(stone)) { int reach = step + stone; if (reach == stones[stones.length - 1]) { return true; } HashSet<Integer> set = map.get(reach); if (set != null) { set.add(step); if (step - 1 > 0) set.add(step - 1); set.add(step + 1); } } } return false; } }

LeetCode [318] Maximum Product of Word Lengths

 318. Maximum Product of Word Lengths

Medium

Given a string array words, find the maximum value of length(word[i]) * length(word[j]) where the two words do not share common letters. You may assume that each word will contain only lower case letters. If no such two words exist, return 0.

Example 1:

Input: ["abcw","baz","foo","bar","xtfn","abcdef"]
Output: 16 
Explanation: The two words can be "abcw", "xtfn".

Example 2:

Input: ["a","ab","abc","d","cd","bcd","abcd"]
Output: 4 
Explanation: The two words can be "ab", "cd".

Example 3:

Input: ["a","aa","aaa","aaaa"]
Output: 0 
Explanation: No such pair of words.

 

Constraints:

• 0 <= words.length <= 10^3
• 0 <= words[i].length <= 10^3
• words[i] consists only of lowercase English letters.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

class Solution { public static int maxProduct(String[] words) { if (words == null || words.length == 0) return 0; int len = words.length; int[] value = new int[len]; for (int i = 0; i < len; i++) { String tmp = words[i]; value[i] = 0; for (int j = 0; j < tmp.length(); j++) { value[i] |= 1 << (tmp.charAt(j) - 'a'); } } int maxProduct = 0; for (int i = 0; i < len; i++) for (int j = i + 1; j < len; j++) { if ((value[i] & value[j]) == 0 && (words[i].length() * words[j].length() > maxProduct)) maxProduct = words[i].length() * words[j].length(); } return maxProduct; } }

LeetCode [632] Smallest Range Covering Elements from K Lists

632. Smallest Range Covering Elements from K Lists

Hard

You have k lists of sorted integers in non-decreasing order. Find the smallest range that includes at least one number from each of the k lists.

We define the range [a, b] is smaller than range [c, d] if b - a < d - c or a < c if b - a == d - c.

 

Example 1:

Input: nums = [[4,10,15,24,26],[0,9,12,20],[5,18,22,30]]
Output: [20,24]
Explanation: 
List 1: [4, 10, 15, 24,26], 24 is in range [20,24].
List 2: [0, 9, 12, 20], 20 is in range [20,24].
List 3: [5, 18, 22, 30], 22 is in range [20,24].

Example 2:

Input: nums = [[1,2,3],[1,2,3],[1,2,3]]
Output: [1,1]

Example 3:

Input: nums = [[10,10],[11,11]]
Output: [10,11]

Example 4:

Input: nums = [[10],[11]]
Output: [10,11]

Example 5:

Input: nums = [[1],[2],[3],[4],[5],[6],[7]]
Output: [1,7]

 

Constraints:

• nums.length == k
• 1 <= k <= 3500
• 1 <= nums[i].length <= 50
• -105 <= nums[i][j] <= 105
• nums[i] is sorted in non-decreasing order.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

class Solution { int[] minRange = new int[2]; int l, r, n; void update(){ if(r-l<minRange[1]-minRange[0]){ minRange[0] = l; minRange[1] = r; } } public int[] smallestRange(List<List<Integer>> nums) { n = nums.size(); l = Integer.MAX_VALUE; r = Integer.MIN_VALUE; PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->(Integer.compare(a[0], b[0])));//value, col, row for(int i=0; i<n; ++i){ int v = nums.get(i).get(0); pq.add(new int[]{v, i, 0}); l = Math.min(l, v); r = Math.max(r, v); } minRange[0] = l; minRange[1] = r; while(true){ int[] top = pq.poll(); int col = top[1], row = top[2]; if(row == nums.get(col).size()-1) break;//the min value reach the last of the list int v = nums.get(col).get(row+1); pq.add(new int[]{v, col, row+1}); l = pq.peek()[0]; r = Math.max(r, v); update(); } return minRange; } }